Designing Computational Textiles with Processing.
Overview
This tutorial will show you how to design textiles using code, specifically the Processing software. Using code makes it easy to create complex and precise patterns that would be difficult to draw manually – and to quickly explore a lot of different variations.
Step 1. Download and Run Processing
Get started by downloading the Processing software, move it to a convenient location (like your Applications or Program Files folder) and run it.
Step 2. Install the WOVNS Processing Examples
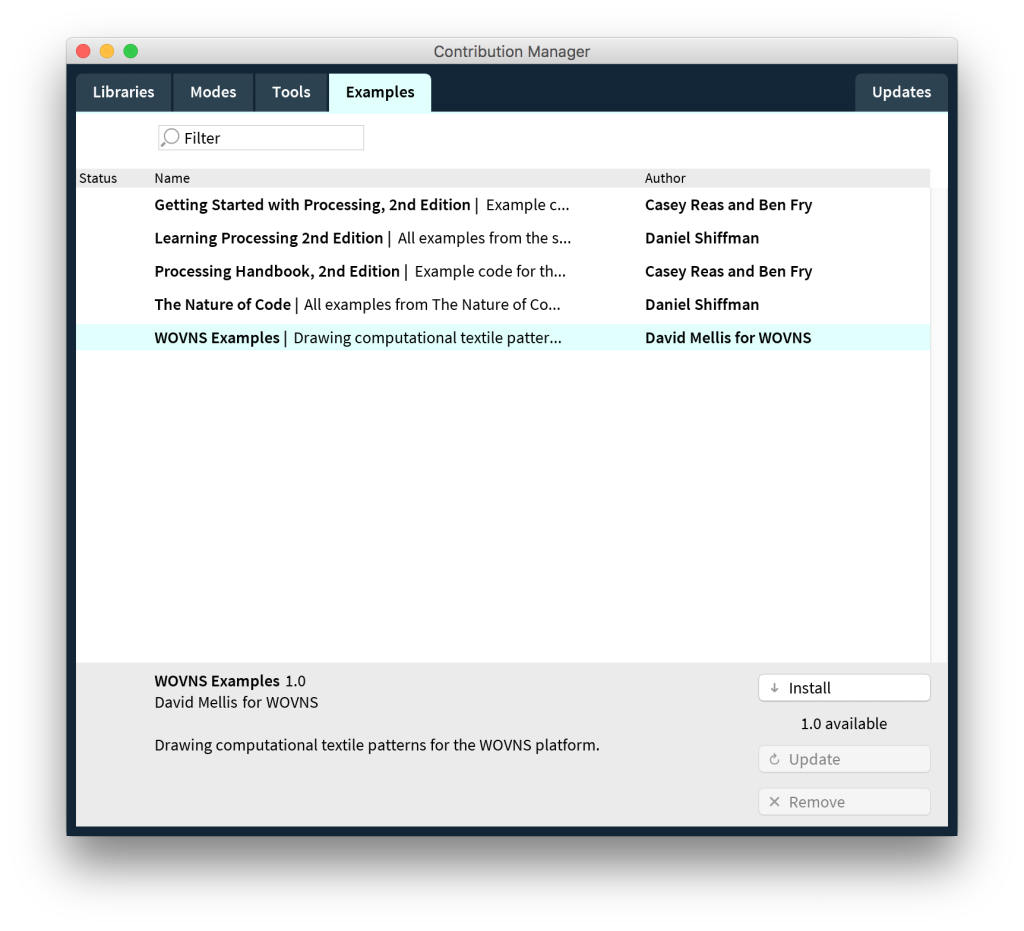
You can install the WOVNS examples using the Processing Contributions Manager. Go to the File > Examples menu item to open the examples window. Then click the Add Examples… button. You should see the examples tab of the contribution manager (pictured below). Click on WOVNS Examples, then click the Install button. Once the installation is complete, you can close the contribution manager.
Step 3. Browse the Examples
You should now see the WOVNS examples inside the “Contributed Examples” section of the examples dialog. (Again, you can open the examples window with the File > Examples… menu item.)
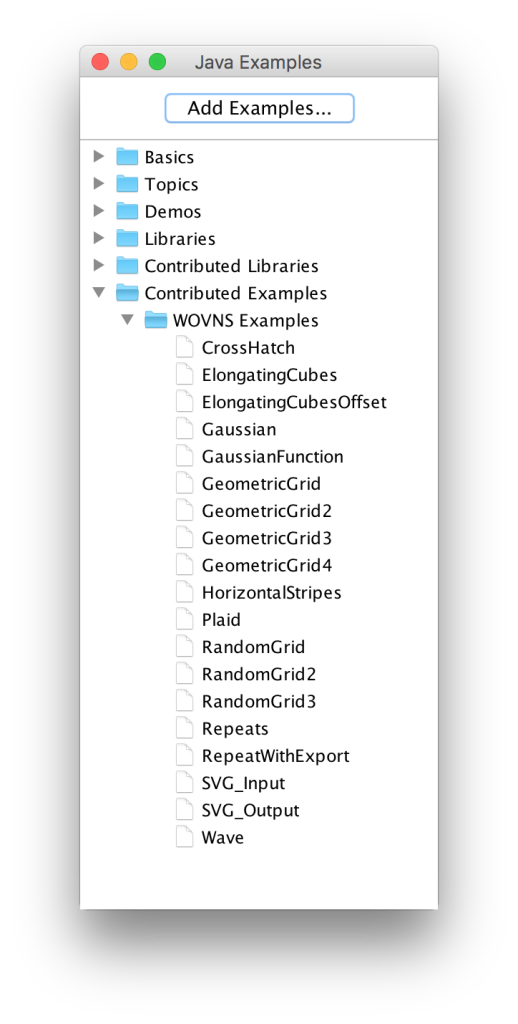
Step 4. Run One of the Examples
Double-click the name of one of the example to open it, then click the play button to run it. You’ll see a new window open showing the pattern generated by the example code. (Here, we show the GeometricGrid example that we’ll explain in more detail next.)

Step 5. Open the Generated PNG File
The window showing the output of the Processing program may be too large to fit on your screen. That’s because weaving is a precise process requiring a high resolution image. Don’t worry! The program also generates a PNG file that you can view with whatever program you like. To get to the PNG, first close the output window and go back to the window showing the code for the example. Then select Sketch > Show Sketch Folder. This will open the folder containing the sketch code itself (a .pde file) plus the PNG file it generated.
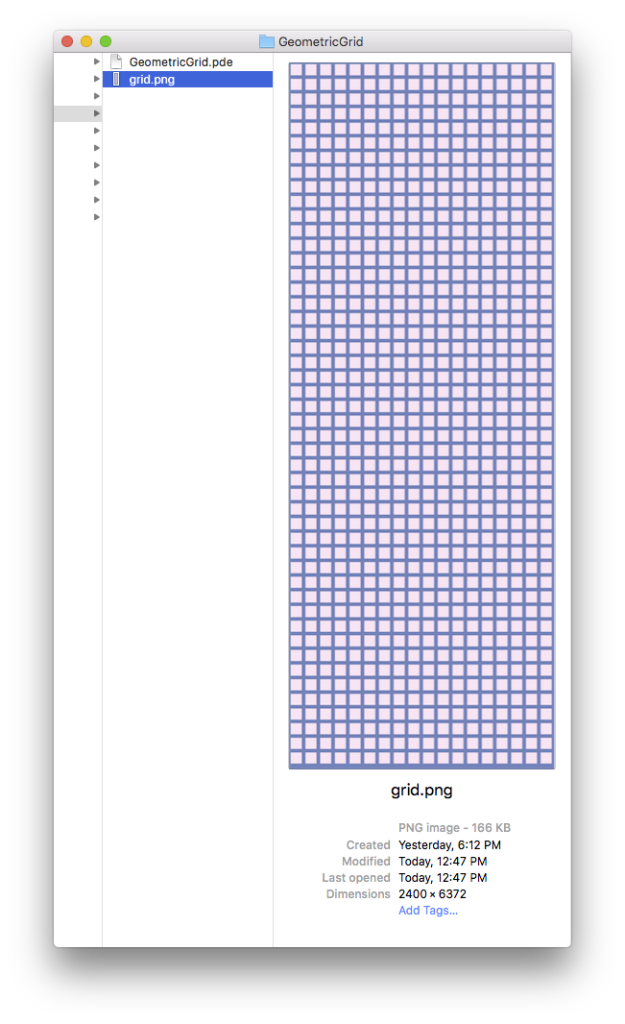
Step 6. Explore the Code
Now that you’ve seen what the example does, it’s time to start playing with the code. The GeometricGrid example (shown in the preceding steps) is a good place to start as it’s a relatively simple. Here, we’ll walk you through the basic elements of that program.
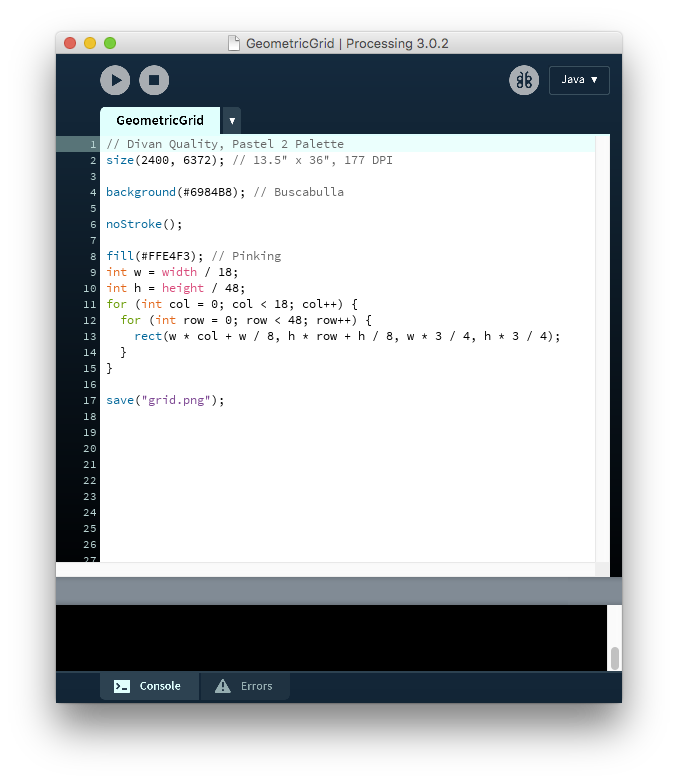
// Divan Quality, Pastel 2 Palette
This line is a comment (indicated by the //). That means it’s there for people to read; the computer ignores it when you run the program. Here, we’ve indicated which WOVNS quality and color palette we’re using (Divan Pastel 2). That’s important because it tells us the size of the PNG we should be generating and the colors we can use.
size(2400, 6372); // 13.5" x 36", 177 DPI
This line calls the size() function to tell Processing how big of an image we want to create. In this case, we’re using the dimensions for the Divan quality, 2400 pixels wide by 6372 pixels high. As we’ve noted in the comment, this corresponds to 13.5″ x 36″ at 177 DPI, and will be repeated four times horizontally for a total width of 54″.
background(#6984B8); // Buscabulla
This line sets the background color of the image using the background() function. Note that we’re specifying the color using a hex code from our chosen palette.
noSmooth();
Tell Processing not to use antialiasing when drawing. This will prevent the use of pixels of various colors at the edges of shapes, which wouldn’t be handled properly in weaving.
fill(#FFE4F3); // Pinking
This line of code uses the fill() function to specify the color that will be used to fill the shapes we draw later on in the program. Again, we’ve chosen a hex code from the Pastel 2 palette.
noStroke();
We use the noStroke() command to tell Processing not to draw outlines around our shapes, since those thin lines wouldn’t work well in our woven textile.
Step 6. Explore the Code (cont…)
Our program is going to draw a grid, 18 columns wide and 48 columns high. First, we calculate the width and height of each cell in the grid:
int w = width / 18; int h = height / 48;
To get the width, we divide the total width of the image (stored in the special variable width) by the number of columns (18). This gives a value of 133 pixels, which is about 0.75″ at 177 DPI. We store this value in the variable w an integer (int). Similarly, we calculate the height of each cell in our grid by dividing height by 48, and store the result in h.
for (int col = 0; col < 18; col++) {
for (int row = 0; row < 48; row++) {
rect(w * col + w / 8, h * row + h / 8,
w * 3 / 4, h * 3 / 4);
}
}
This code is the core of the program. It loops through the 18 columns of our grid and, for each column, loops through the 48 rows of the grid. For each row in each column, it draws a rectangle (actually a square) using the rect() function. To explain how it works, let's look in detail at each of its parts.
for (int col = 0; col < 18; col++)
This is a for-loop, which repeats a section of code multiple times. It has three parts:
- int col = 0: the initialization portion, which runs once, the first time through the for loop. In this case, the initialization consists of creating an integer variable called col and setting its value to 0.
- col < 18: the test portion, which specifies the conditions under which the for-loop should continue to execute. The test is evaluated once for each iteration through the loop, if it's true, the loop runs again, if it's false, the loop ends. In this case, the test means that the loop will run as long as the value of col is less than 18.
- col++: the increment portion of the loop, which runs at the end of each pass through the for-loop. This code uses the ++ operator to add one to the value of col.
The overall effect of this code is to run the body of the loop (the code between the { and }) 18 times. The first time through the loop col is 0 (as specified in the initialization portion of the loop). After the loop runs once, the increment code (col++) runs, changing the value of col to 1. Then the test executes, checking if col is less than 18, which it is. So the loop runs for a second time, with col set to 1. Then col is incremented to 2 and the loop runs for a third time, and so on, until col is 17 (the 18th time through the loop). At the end of that iteration, col is incremented to 18, meaning that (col < 18) is no longer true, so the loop ends.
for (int row = 0; row < 48; row++)
This inner loop is similar, except that it runs for each value of the row variable from 0 to 47. Note that because this loop is inside the body of the outer (col) loop, it runs once for each time through that outer loop. That is, for each column from 0 to 17, we iterate through rows 0 to 47.
Step 6. Explore the Code (cont...)
Here's a diagram of the grid:
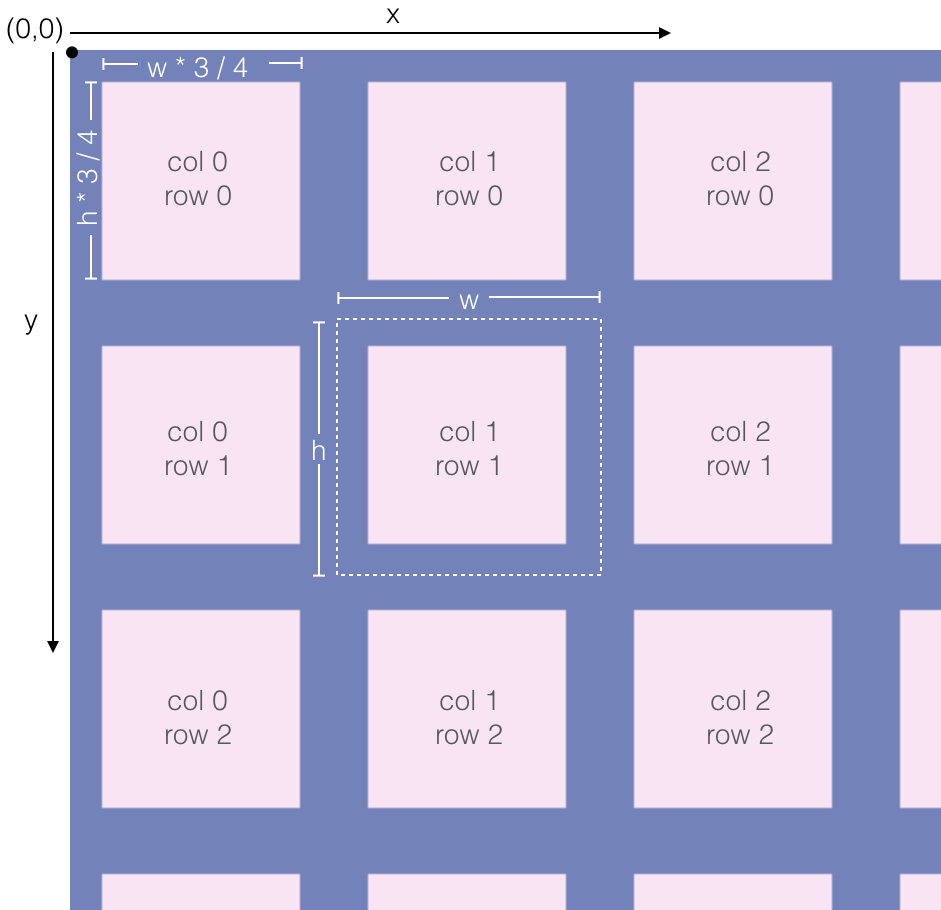
rect(w * col + w / 8, h * row + h / 8,
w * 3 / 4, h * 3 / 4);
Here's the inside of the two loops, the rect() function. It runs 18 * 48 (864) times, drawing a square each time. The first two arguments to rect(), w * col + w / 8 and h * row + h / 8 specify the x and y coordinates of the upper left corner of the rectangle. Because the x coordinate includes w * col, each time col increases by 1, the x coordinate will increase by w – that is, the rectangle will start w pixels to the right of the previous one. Similarly, each time row increases by 1, the rectangle will move down by h pixels. (The origin, or (0, 0) point of the screen is in the upper left corner.) We add w / 8 to the x-coordinate and h / 8 to the y-coordinate to center the square within the cell of the grid. (The square is 3/4 the size of the cell, so we want it to have a margin of 1/8 of the cell on every side.)
The next two arguments to rect(), w * 3 / 4 and h * 3 / 4 specify the width and height of the rectangle (in pixels). Here, we make the width of our square 3/4 the size of our cell width and its height 3/4 the height of the cell.
save("grid.png");
The last line of the program calls Processing's save() function to output a PNG file containing the pattern generated by the code. You can find the resulting file in the folder that contains your program. Again, you can use the Sketch > Show Sketch Folder menu item to open that folder.
Step 7. Create Alternating Patterns
The GeometricGrid2 example is almost the same as the previous example, except that we've changed half of the squares into ellipses.
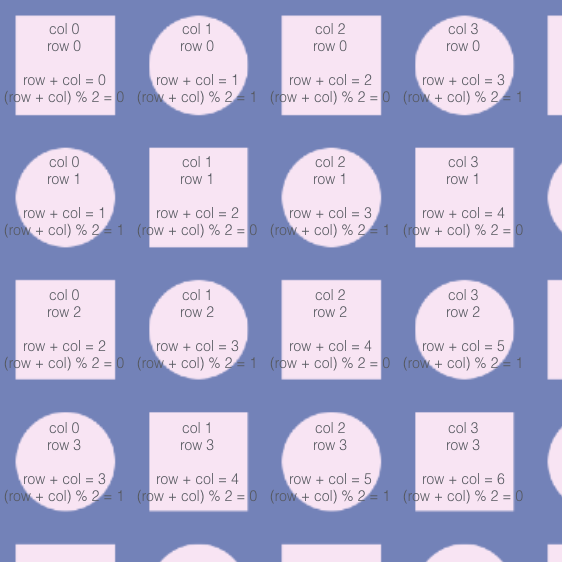
The code for this example is almost the same, with a couple of changes. First of all, we use an if-statement to decide whether to draw a square or a circle:
if ((row + col) % 2 == 0) {
rect(w * col + w / 8, h * row + h / 8,
w * 3 / 4, h * 3 / 4);
} else {
ellipse(w * col + w / 8, h * row + h / 8,
w * 3 / 4, h * 3 / 4);
}
If the condition (row + col) % 2 == 0 (which we'll explain in a second) is true, we call rect() to draw a square; otherwise (else), we call ellipse() to draw a circle. Now let's look at the condition itself:
(row + col) % 2 == 0
This uses the modulo operator (%), which gives the remainder when one number is divided by another (e.g. 21 % 9 is 3, because when 21 is divided by 9, the remainder is 3). Here, we look at the remainder when (row + col) is divided by two; this will be 0 when (row + col) is even and 1 when it's odd. Note that if (row + col) is, say, even, adding one to either row or col will give an odd sum – meaning that (row + col) % 2 alternates between 0 and 1 as you go across a row or down a column. That means that our code alternates between drawing squares and drawing circles.
Now let's look at the code to draw the circle:
ellipse(w * col + w / 8, h * row + h / 8,
w * 3 / 4, h * 3 / 4);
Notice that the arguments to ellipse() are the same as the arguments to rect(). This is because we've set up the ellipse() function to work the same as rect(), i.e. the first two arguments specify the upper-left corner of the ellipse (or circle, in this case) and the next two arguments specify its width and height. Note that by default in Processing the first two arguments of the ellipse() function specify its center, so we used ellipseMode() earlier in the program to allow us to specify the upper-left corner instead:
ellipseMode(CORNER);
Step 8. Create Random Patterns
The RandomGrid example adds a little bit of randomness to generate a much more complex pattern. It starts to show how we can take advantage of programming to create new and interesting designs. This example is based on a pattern by Bonny Guo.
Let's look at the code. Here's the start of the program:
size(3984, 3000); // 46.5" x 36", 84 DPI background(#020100); // Textured noSmooth(); stroke(#A53643); // Cranberry strokeWeight(15); noFill();
This is similar to what we've seen in the other examples. It configures the canvas and specifies how the shapes that appear later in the program should be drawn. In this case, though, we're using the Talma quality, Spectrum 12 palette. As a result, we use the size() command to set the canvas to 3984 pixels wide by 3000 pixels high. The Talma quality has a full-width repeat, so this corresponds to the full size of a yard of fabric, 46.5" wide by 36" high, at 84 DPI. We set the background color to "Textured", one of the Spectrum 12 colors. As in the other examples, we call noSmooth() to disable anti-aliasing, as that would interfere with the appearance of the woven fabric. Finally, in this example we're drawing outlines for the shapes but not filling in their insides, so we set the stroke() to "Cranberry" and call the noFill() command. We use the strokeWeight() command to set the thickness of the outlines of our shapes to 15 pixels, or about 1/6" at 84 DPI.
As in the other examples, this code is based on a grid. Let's look at the code that creates the grid:
int m = 84;
for (int y=0; y<height; y+=m) {
for (int x=0; x<width; x+=m) {
// ...
}
}
As before, we use two for-loops to iterate through each cell of the grid. (For now, I've replaced the body of the loops with a comment reading ....) Here, though, we keep track of the x and y coordinate (in pixels) of each cell in the grid. The m variable stores the size of the (square) grid cells, 84 pixels or 1" (in both width and height). Each time through the outer loop, we use the code y+=m to increment y by 84 (the value of m), moving 1" down the canvas. Each time through the inner loop, we use x+=m to increment x by 84 and move 1" across the canvas. The repeats until we reach the bottom right edge of the canvas.
Step 8. Create Random Patterns (cont...)
Now let's take a look at the code that runs for each cell of the grid (the code in the ... above). We want to draw a different random shape for each cell of the grid. First, we need to pick a random number:
int j=int(random(9));
This line of code asks Processing to randomly pick one of 9 numbers: 0, 1, 2, 3, 4, 5, 6, 7, or 8. (Computers like to start counting at 0.) We store the result in the variable j.
Now, we use an if-statement to draw different shapes depending on the value of j:
if (j==1) {
ellipse(x+0.5*m, y+0.5*m, m, m);
} else if (j==2) {
line(x, y+0.5*m, x+0.5*m, y+0.5*m);
line(x+0.5*m, y+0.5*m, x+0.5*m, y);
} else if (j==3) {
// ...
}
(Again, here I've replaced part of the code with .... It's largely a repeat of what's already here.)
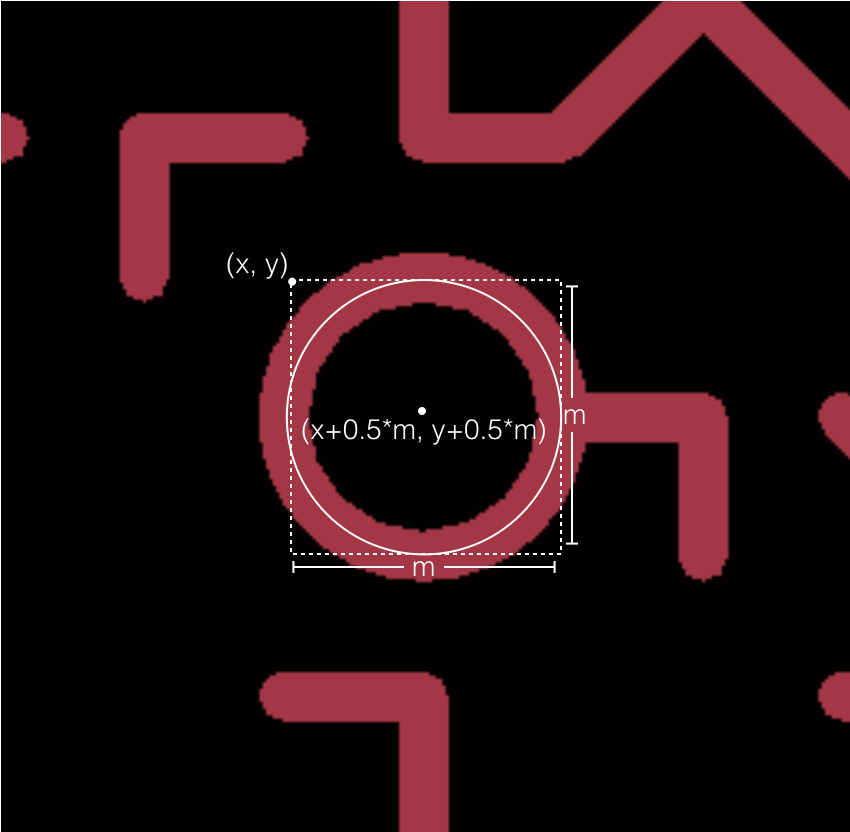
If j is 1 – that is, if the random() function randomly chose the number 1 – we draw an ellipse. As before, we specify the x and y coordinates of the center of the ellipse, x+0.5*m and y+0.5*m, along with its width and height, which are both m (84 pixels or one inch). That is, the ellipse is actually a circle, filling the full grid cell. Here's a diagram (the white dotted lines show the cell of the grid):
The point (x, y) is in the upper-left corner of the grid cell, which is m pixels wide and m pixels high. The center of the ellipse is at (x + 0.5*m, y + 0.5*m) – half-way across the cell and half-way down it.
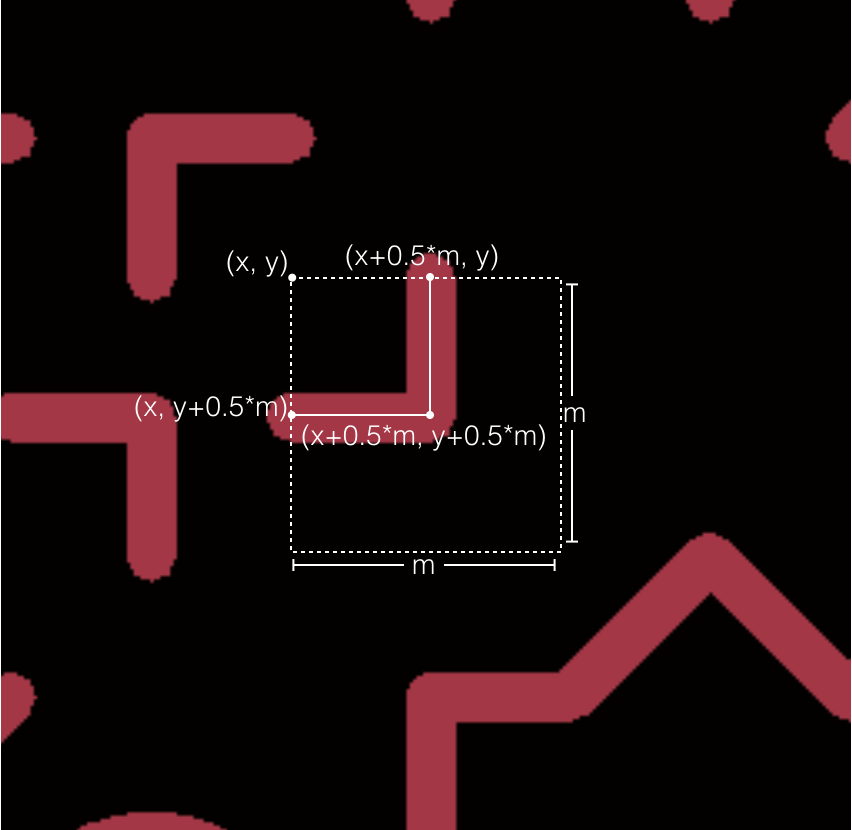
If j is 2, our code draws two lines in the grid cell:
line(x, y+0.5*m, x+0.5*m, y+0.5*m); line(x+0.5*m, y+0.5*m, x+0.5*m, y);
The Processing line() command draws a line between two points. It takes four parameters, the x and y coordinate of the start of the line and the x and y coordinate of the end of the line. Here's a diagram:
Step 8. Create Random Patterns (cont...)
The rest of the code draws different combinations of two lines, depending on the random number stored in the variable j. As in the other examples, the last line of the program saves the resulting image:
save("random.png");
Be sure to check out the RandomGrid2 and RandomGrid3 examples. The code is almost the same as RandomGrid, but they generate completely different patterns with very different aesthetics (shown at the top of this tutorial). These examples are a great basis for your experiments!
Step 9. Explore the Other Examples
Now that you've gotten a taste of using Processing to generate textile patterns, take a look at other examples. Try running them to see what pattern it generates. Experiment with changing the code to get different results. Keep playing until you create a design you like. Remember to use the size and colors from one of the WOVNS qualities and color palettes.
Diagram for the CrossHatch example.
Step 10. Upload Your Design to WOVNS
Once you've settled on a design you like, take the PNG generated by Processing, upload it to WOVNS, and order your fabric!
Step 11. Learn More about Processing
To learn more about Processing, check out the following resources:
- Processing Tutorials: great explanations on a wide range of topics
- Processing Reference: details of each element in the Processing language
- Processing Books: from a wide range of authors